科学无止境，探索永不停。同学们大家好，欢迎来到今天的探秘小课堂。在浩瀚的知识海洋中，隐藏着无数的秘密与奇迹，它们如同璀璨的星辰，等待着我们去发现、去探索。今天，就让我们带着好奇心与求知欲，走进这个探秘小课堂吧。

同学们，想象一下，在铺满橡子的小径上，一辆看似简单却设计巧妙的滑车，无需复杂的机械结构，仅凭其独特的形状，便能平稳地穿梭于曲折之间，这便是橡子车辊的魅力所在。它不仅仅是一个玩具，更是一把几何美学与物理原理融合之门的钥匙，那就让我们通过身后的这件展项《橡子车辊》开启吧。

展品讲解第二课

视频来源于科普大巴扎

《橡子车辊》

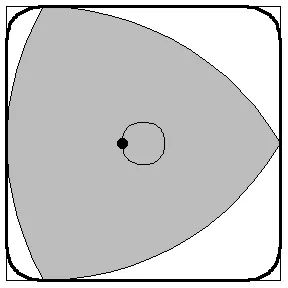
橡子车辊轨道里的物体它的名字叫橡子，形状就像我们的这个变胖的三角形，我们把它叫做勒洛三角形。当小车在上面运动时，可以平稳前进，下面的橡子也可以像球一样平稳滚动。

勒洛三角形：也译作莱洛三角形或弧三角形，又被称为划粉形或曲边三角形，是除了圆形以外，最简单易懂的勒洛多边形，一个定宽曲线。将一个曲线图放在两条平行线中间，使之与这两平行线相切，则可以做到：无论这个曲线图如何运动，只要它还是在这两条平行线内，就始终与这两条平行线相切。这个定义由十九世纪的德国工程师Franz Reuleaux命名。

实际应用：

井盖和稳定搬运：由于勒洛三角形的定宽性质，它可以作为井盖使用，防止井盖掉入下水道。它也可以用于稳定地搬运物品，因为其形状在滚动时不会发生上下抖动。

轮子设计：

尽管勒洛三角形在理论上可以用作轮子，但由于其旋转中心的高度不固定，可能会导致在颠簸的路面上行驶时不稳定。然而，勒洛三角形形状的钻头可以钻出近似正方形的孔，这在某些工业应用中可能很有用。

发动机设计：

勒洛三角形的形状特性使其适用于设计转子发动机，这种发动机能够更高效地完成进气、压缩、做功和排气的工作，从而提高马力和容积比。

其他工业应用：

在制造领域，勒洛三角形可用于设计各种机械零件，例如在扫地机器人中。其定宽性质也使得它在需要稳定宽度的场合非常有用，比如在某些传输带的设计中。

艺术和设计：

勒洛三角形由于其独特的形状，在艺术和设计中可以作为装饰元素。例如，在乐高版勒洛三角形的应用中，可以看到它被用于创建有趣的动态效果和轨迹。

数学和几何研究：

勒洛三角形是定宽曲线中面积最小的图形，这一性质在数学和几何学研究中具有一定的意义。

综上所述：勒洛三角形由于其独特的形状和性质，在工程、制造、艺术和设计等多个领域都有实际应用。虽然它可能在某些方面（如作为轮子）存在局限性，但其创新性和多功能性使其成为一个值得研究的几何形状。